Stell dir vor, du planst eine Brücke und beschreibst diese mit einer Funktion . Dann wäre es doch cool, du könntest die Brückenlänge bzw. die Länge des Brückenbogens ganz einfach ausrechnen.
Lerne mit Millionen geteilten Karteikarten
Leg kostenfrei los
Schreib bessere Noten mit StudySmarter Premium
Geld-zurück-Garantie, wenn du durch die Prüfung fällst
Review generated flashcards
Erstelle unlimitiert Karteikarten auf StudySmarter
Team Bogenlänge Lehrer
Damit du in das Thema Bogenlänge gleich voll einsteigen kannst, schau dir vorher die Artikel zu den Themen Ableitungsregeln und Integralen an.
Wie vorhin schon angedeutet, können wir mithilfe der Bogenlänge sogar bauliche Strukturen berechnen. Aber was genau ist denn mathematisch überhaupt die Bogenlänge?
Die Bogenlänge einer ebenen Kurve beschreibt die Länge der Kurve zwischen den beiden Punkten A und B.
In der Mathematik werden meist die Bogenlängen von Funktionsgraphen betrachtet. Sehen wir uns doch dazu gleich mal ein Beispiel an, um das Thema besser verstehen zu können.
Die Abbildung 1 zeigt dir den Funktionsgraphen einer Funktion . Zudem sind zwei Punkte A und B eingezeichnet. Ebenfalls werden die x-Werte der Punkte A und B als klein a und klein b markiert.
Wenn wir den Graphen von Punkt A zu Punkt B nachzeichnen würden, dann ergibt sich die orange Kurve. Genau diese orange ebene Kurve stellt die Bogenlänge L dar und zwar in dem Intervall .
Gut, damit weißt du bereits, was genau die Bogenlänge ist. Und wie können wir diese berechnen?
Bei einfachen Graphen können wir die Bogenlänge L sogar mit dem Satz des Pythagoras berechnen. Weißt du noch, wie sich dieser zusammensetzt?
Kurze Wiederholung: Der Satz des Pythagoras lautet: , wobei a und b Katheten und c die Hypotenuse eines rechtwinkligen Dreiecks sind.
Wir zeigen dir später gleich ein Beispiel zur Berechnung über den Satz des Pythagoras. Meist ist es aber leider nicht so einfach die Bogenlänge zu berechnen. Daher müssen wir uns einer alternativen Formel bedienen, die für alle Arten von Graphen angewendet werden kann.
Du kannst die Bogenlänge L mit Hilfe eines Integrals berechnen.
Die Bogenlänge L des Kurvenstücks einer Funktion in einem Intervall
kann mit folgender Formel berechnet werden:
In der Formel ist dabei die erste Ableitung der Funktion
.
Du musst dir die Bogenlänge als die Länge vorstellen, die du auf einem Graphen zwischen zwei Punkten ablaufen kannst.
Klingt ganz schön kompliziert, oder? Sehen wir uns zusammen zwei Beispiele an, um die Formel verstehen und anwenden zu können.
Wie oben bereits erwähnt, gibt es Funktionen, bei denen es relativ einfach ist eine Bogenlänge auf dem Graphen zu bestimmen. Bei linearen Funktionen kann uns statt der allgemeinen Formel auch der Satz des Pythagoras weiterhelfen.
Gegeben sei die Funktion mit
. Berechne die Länge L der Kurve in dem Intervall
.
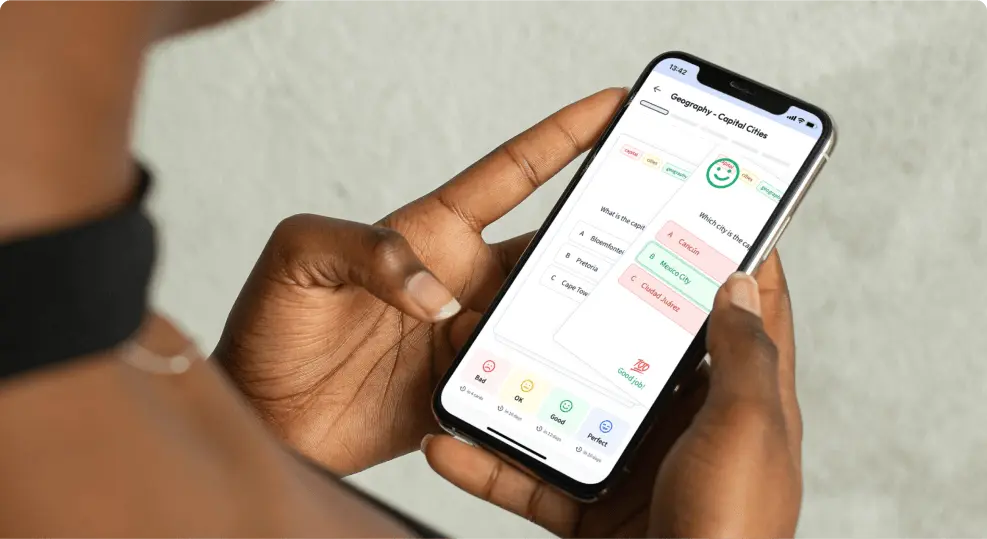
Um dir das Beispiel besser vorstellen zu können, kannst du dir die folgende Abbildung 2 ansehen. Wir zeichnen darin sowohl den Funktionsgraph als Gerade ein und außerdem die Anfangs- und Endpunkte A und B des Intervalls auf dem Graphen.
Der Bogen (oder in diesem Fall hier die Strecke) zwischen den Punkten A und B ist die gesuchte Bogenlänge.
In diesem Fall haben wir zwei Möglichkeiten zur Berechnung der Bogenlänge:
Wir sehen uns beide Varianten an und überprüfen, ob wir das gleiche Ergebnis erhalten.
Da es sich um eine Gerade handelt, können wir den Bogen zwischen Punkt A und Punkt B als Strecke bezeichnen. Zeichnen wir nun ein rechtwinkliges Dreieck mit der Bogenlänge L als Hypotenuse ein, so können wir mithilfe der Formel zum Satz des Pythagoras den Bogen berechnen.
Wie du in der Abbildung 3 sehen kannst, lassen sich die Längen der Katheten ganz einfach berechnen.
Mit Hilfe des Satzes des Pythagoras
kannst du nun die Bogenlänge L berechnen. In der Formel entspricht die Länge L der Hypotenuse c. Die jeweiligen Katheten sind hier und
. Also gilt folgende Formel:
Setzen wir die errechneten Zahlenwerte der Katheten in die Formel ein, so erhalten wir als Lösung:
Vergiss nicht zum Schluss die Einheit hinzuzufügen. Wir berechnen hier schließlich eine Länge und diese benötigt eine Längeneinheit LE.
Durch den Satz des Pythagoras konnten wir die Bogenlänge L leicht berechnen. Durch Berechnung über die allgemeine Formel zur Bogenlänge müssten wir das gleiche Ergebnis erhalten. Lass uns das zusammen überprüfen.
In diesem Fall müssen wir unsere Grenzen des Intervalls betrachten. Das sind die x-Werte zu den Punkten A und B.
Bitte nicht verwechseln mit den Buchstaben aus dem Satz des Pythagoras!
Zur Veranschaulichung kannst du dir folgendes Bild ansehen.
Hierbei ist der x-Wert des Punktes A der Beginn des Intervalls und der x-Wert des Punktes B das Ende des Intervalls. In unserem Fall ist das allgemeine Intervall also
, da gilt:
und
.
Nehmen wir jetzt unsere allgemeine Formel zur Berechnung der Bogenlänge L her.
In diese können wir unsere untere und obere Grenze des Integrals bereits einsetzen. Klein a ist dabei die untere Grenze, weshalb ist. Daraus folgt, dass
gilt.
Jetzt fehlt nur noch die 1. Ableitung unserer Funktion f(x).
Falls du dir hierbei nicht mehr ganz sicher bist, wie du Funktionen ableiten kannst, sieh dir unseren Artikel zu den Ableitungsregeln an. Für die Ableitung gilt:
Setzt du nun die Ableitung f'(x) in die Formel ein, erhältst du Folgendes:
Als Nächstes musst du die Stammfunktion bilden und den Hauptsatz der Differential- und Integralrechnung anwenden. Auch hier kannst du dir bei Fragen wieder unseren Artikel zum Thema Stammfunktion bilden anschauen.
Wie du sehen kannst, kommst du mit beiden Methoden zur selben Bogenlänge L. Leider funktioniert der Satz des Pythagoras nur bei Geraden.
Bei den meisten Aufgaben ist es durch die Wurzel händisch nicht oder nur schwer möglich eine Stammfunktion zu bilden. Deshalb kannst du hier einen Taschenrechner verwenden.
Wie du sicher bemerkt hast, wird in der Formel die Ableitung von der Funktion
genutzt. Das heißt, existiert an einem Punkt im Intervall keine Ableitung
, dann kannst du die Bogenlänge L der Kurve nicht mit der Formel berechnen. Die Funktion
ist also in diesem Intervall nicht differenzierbar.
Dementsprechend kannst du beispielweise die Bogenlänge L im Intervall für die Betragsfunktion
mit
nicht mit der Formel berechnen, da am Punkt keine Ableitung
existiert.
Sehen wir uns noch ein zweites Beispiel mit einer ganzrationalen Funktion an.
Gegeben sei die Funktion mit
. Berechne die Bogenlänge L der Kurve auf dem Intervall .
Schau dir den Funktionsgraphen der Funktion zuerst einmal im Koordinatensystem an. Wie du vielleicht festgestellt hast, handelt es sich hierbei um die Funktion
, die bereits als Eingangsbeispiel erwähnt wurde.
Unsere obere und untere Grenze des Intervalls und damit auch des Integrals wissen wir bereits aus der Aufgabenstellung. Es gilt: .
Zudem bilden wir wieder die Ableitung der Funktion
.
Als Nächstes setzt du alle gegebenen Werte in die Formel ein.
Da du dieses Integral nicht von Hand lösen kannst, darfst du dies mit dem Taschenrechner lösen. Als Bogenlänge L erhalten wir demnach:
Super, wir können damit schon die Bogenlänge von verschiedenen Funktionsgraphen berechnen. Aber wieso funktioniert das überhaupt mit dieser allgemeinen Formel und wie kann man sich mathematisch dieser Bogenlänge annähern?
Um dir die Bogenlänge etwas verständlicher zu machen, schauen wir uns eine Annäherung an. Die Punkte A und B stellen wieder die Anfangs- und Endpunkte auf dem Graphen dar. Der Bogen dazwischen ist die Bogenlänge L.
Gesucht ist bei der gezeichneten Funktion f(x) wieder eine Bogenlänge L in dem allgemeinen Intervall bzw. hier
.
Dieses große Intervall teilen wir in mehrere Teilintervalle der Längeauf. In diesem Bild sind diese
. Die Punkte auf dem Graphen bei den jeweiligen x-Werte sind damit bei den Stellen:
Jetzt könnten wir für jede Strecke die Länge mit Hilfe des Satz des Pythagoras ausrechnen und alle Ergebnisse addieren.
Allerdings kannst du sehen, dass die Strecken sich nicht mal näherungsweise an dem Funktionsgraphen befinden.
Deshalb wählen wir im nächsten Bild mehr Intervalle mit einer kleineren Größe. Du hast jetzt fünf Intervalle mit der Länge .
Du siehst nun, dass sich die Strecken weiter annähern. Allerdings siehst du immer noch, dass es genügend Strecken gibt, die sehr unterschiedlich zu dem Graphen sind.
Deshalb wählen wir noch einmal mehr Intervalle, die noch kleiner sind. Im nächsten Bild siehst du 15 Intervalle mit der Länge .
Inzwischen näher sich die Strecken dem eigentlichen Funktionsgraphen und damit der Bogenlänge gut an.
Um nun die exakte Bogenlänge L zu erhalten, müsste man die Anzahl der Intervalle unendlich groß wählen und damit die Größe der Intervalle gegen 0 laufen lassen. Dies ist mathematisch nur mit der Berechnung eines Integrals möglich, weshalb die allgemeine Formel zur Berechnung der Bogenlänge L auch keine Summenformel, sondern ein Integral in einem bestimmten Intervall ist.
Die grundlegende Vorgehensweise der schrittweisen Berechnung der Bogenlänge hast du damit bereits gesehen. Interessiert dich der genaue Zusammenhang zur allgemeinen Formel? Dann sieh dir unsere Vertiefung an.
Sehen wir uns den Graphen der Funktion noch einmal genauer an. Zur Erklärung und Herleitung betrachten wir dazu einen Teilbogen L im Intervall
auf dem Funktionsgraphen.
Wie du vorhin bereits gesehen hast, können wir zunächst einmal den direkten Weg von Punkt A zu Punkt B verbinden und damit eine Strecke bilden. Berechnen lässt sich diese Strecke mithilfe des Satzes des Pythagoras.
Unsere Strecke ist dabei die Hypotenuse und die beiden anderen Seiten
und
sind die zugehörigen Katheten. Wir können damit folgende Gleichung definieren:
Als Nächstes zeichnen wir eine Tangente an den Funktionsgraphen, die parallel zur Strecke ist. Den zugehörigen x-Wert, an dem die Tangente den Graphen berührt, bezeichnen wir als
.
Würden wir die Steigung der Tangente
berechnen wollen, so können wir dies ebenfalls über
und
tun, da die Tangente parallel zur Strecke
ist. Es gilt also:
Falls du dich noch erinnern kannst, ist die Steigung einer Tangente an einer bestimmten Stelle
gleich der Ableitung der Funktion
an dieser Stelle
. Wir können daher definieren:
Formulieren wir diese neue Gleichung um und lösen sie nach auf, so erhalten wir:
Diese Gleichung setzen wir in die obige Gleichung zur Strecke ein.
Jetzt klammern wir das aus und ziehen es vor die Wurzel.
Die Strecke können wir demnach mit dieser Formel berechnen. Wie du in den Abbildungen sehen kannst, entspricht diese Strecke aber nicht der exakten Länge des Teilbogens L. Sie ist lediglich die direkte Strecke zwischen den Punkten A und B.
Wir wollen aber so nah wie möglich an die Bogenlänge L herankommen, weshalb wir statt einer Strecke im Intervall jetzt zwei Teilstrecken
und
nutzen. Sie dir dazu das folgende Bild an.
Wie du sehen kannst, liegen unsere Teilstrecken auf jeden Fall schon näher an unserem Bogen als die einzelne Strecke vorher. Mit und
berechnen wir diese genauso wie vorher.
Diese können wir wie folgt zusammen, indem wir bei den einzelnen Wurzeln ausklammern und dann wieder vor die Wurzel setzen.
Hier haben wir lediglich zwei Teilstrecken benutzt, um uns der Bogenlänge L anzunähern. Wie du vorhin schon gesehen hast, benötigen wir sehr viele Teilstrecken, um möglichst nahe an die Bogenlänge heranzukommen.
Wir bezeichnen die x-Werte daher mit einer allgemeinen Variable k. Diese beginnt bei 1 (also ) und geht bis zu einer sehr großen Zahl n. Das kann beispielsweise
sein. Damit erhalten wir sehr viele Intervalle und Tangenten (in diesem Fall z. B. 2000 Intervalle). Allgemein können wir daher wie folgt die Summe von sehr vielen Teilstrecken definieren:
Lassen wir die Anzahl der Intervalle jetzt unendlich werden (also n gegen ), dann erhalten wir unendlich viele Abschnitte
und zugehörige Tangenten. Dies ist dann mathematisch nur noch mit der Integralrechnung möglich.
Daher ergibt sich dann für die Bogenlänge L einer Funktion in einem Intervall
:
Auch wenn das anfangs schwierig zu verstehen ist, merke dir: Wenn wir unendlich viele Abschnitte in einem Intervall betrachten, dann greifen wir mathematisch zum Trick des Integrals.
Um deine Fähigkeiten noch einmal anzuwenden, probiere dich an den folgenden zwei Beispielen.
Gegeben sei die Funktion f(x) mit . Berechne die Bogenlänge L der Funktion f(x) auf dem Intervall [-1, 5].
Das Schaubild der Funktion f(x) sieht wie folgt aus.
Zuerst musst du die Ableitung f(x) bilden.
Als Nächstes wird die Ableitungsfunktion sowie die obere und untere Grenze in die Formel eingesetzt.
Entweder du gibst diese Ausdruck schon in den Taschenrechner ein oder du vereinfachst den Ausdruck unter der Formel noch etwas. Allerdings können beim Umformen leicht Fehler entstehen, weshalb du es schon jetzt in den Taschenrechner eingeben solltest.
Als Ergebnis erhalten wir dann:
Gegeben sei die Funktion f(x) mit . Berechne die Bogenlänge L der Funktion
auf dem Intervall
.
Das Schaubild der Funktion sieht wie folgt aus.
Zuerst musst du wieder die Ableitung bilden.
Jetzt kannst du die Gleichung mit den Grenzen in die Formel einsetzen und weiter vereinfachen.
Dieser Ausdruck lässt sich wieder in den Taschenrechner eingeben. Damit ergibt sich die Lösung:
Melde dich kostenlos an, um Zugriff auf all unsere Karteikarten zu erhalten.
Ist das Bogenmaß gleich die Bogenlänge?
Nein, das Bogenmaß ist ein Winkelmaß und die Bogenlänge ist die Länge einer Kurve.
Ist die Bogenlänge der Umfang?
Nein, die Bogenlänge ist die Länge einer Kurve.
Was ist die Bogenlänge?
Die Bogenlänge ist die Länge einer Kurve. Es ist die Länge, die man auf einem Graphen von einem Punkt A zu einem Punkt B ablaufen könnte.
Wie berechnet man die Länge einer Kurve?
Die Länge der Kurve lässt sich mit der allgemeinen Integralformel für die Bogenlänge berechnen.
Bei StudySmarter haben wir eine Lernplattform geschaffen, die Millionen von Studierende unterstützt. Lerne die Menschen kennen, die hart daran arbeiten, Fakten basierten Content zu liefern und sicherzustellen, dass er überprüft wird.
Lily Hulatt ist Digital Content Specialist mit über drei Jahren Erfahrung in Content-Strategie und Curriculum-Design. Sie hat 2022 ihren Doktortitel in Englischer Literatur an der Durham University erhalten, dort auch im Fachbereich Englische Studien unterrichtet und an verschiedenen Veröffentlichungen mitgewirkt. Lily ist Expertin für Englische Literatur, Englische Sprache, Geschichte und Philosophie.
Lerne Lily kennen
Gabriel Freitas ist AI Engineer mit solider Erfahrung in Softwareentwicklung, maschinellen Lernalgorithmen und generativer KI, einschließlich Anwendungen großer Sprachmodelle (LLMs). Er hat Elektrotechnik an der Universität von São Paulo studiert und macht aktuell seinen MSc in Computertechnik an der Universität von Campinas mit Schwerpunkt auf maschinellem Lernen. Gabriel hat einen starken Hintergrund in Software-Engineering und hat an Projekten zu Computer Vision, Embedded AI und LLM-Anwendungen gearbeitet.
Lerne Gabriel kennen